Sub-Goal Trees – a Framework for Goal-Based Reinforcement Learning
ICML 2020
T Jurgenson, O Avner, E Groshev, A Tamar
Many AI problems, in robotics and other domains, are goal-based, essentially seeking
trajectories leading to various goal states. Reinforcement learning (RL), building on
Bellman’s optimality equation, naturally optimizes for a single goal, yet can be made
multi-goal by augmenting the state with the goal. Instead, we propose a new RL
framework, derived from a dynamic programming equation for the all pairs shortest path
(APSP) problem, which naturally solves multigoal queries. We show that this approach
has computational benefits for both standard and approximate dynamic programming.
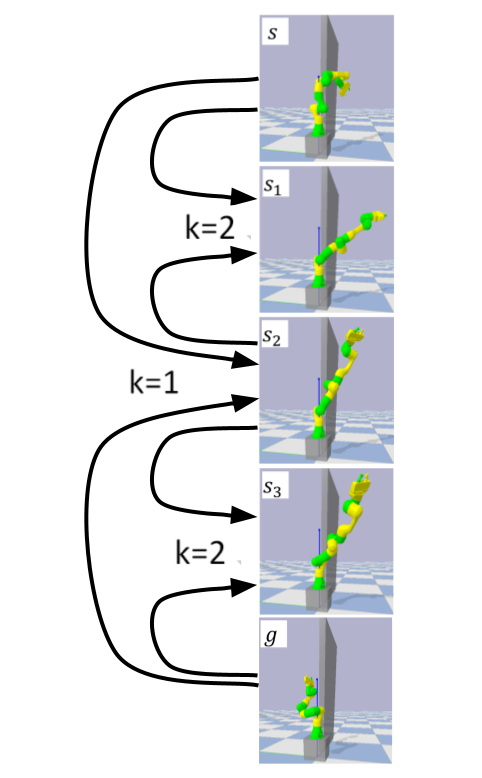
Interestingly, our formulation prescribes a novel protocol for computing a trajectory:
instead of predicting the next state given its predecessor, as in standard RL, a
goal-conditioned trajectory is constructed by first predicting an intermediate state
between start and goal, partitioning the trajectory into two. Then, recursively,
predicting intermediate points on each sub-segment, until a complete trajectory is
obtained. We call this trajectory structure a subgoal tree. Building on it, we
additionally extend the policy gradient methodology to recursively predict sub-goals,
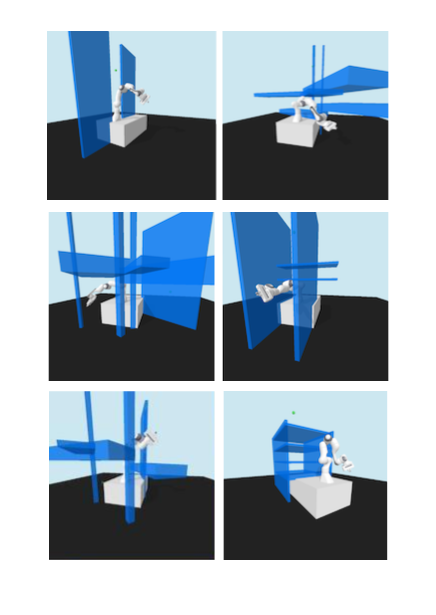
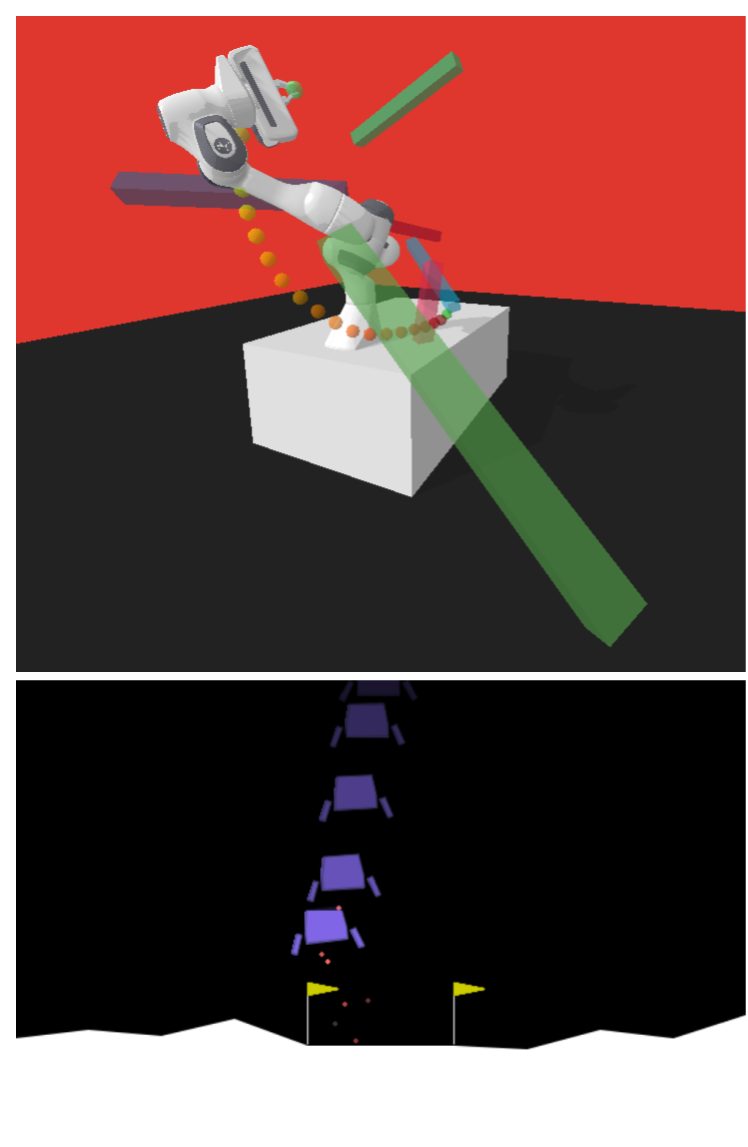
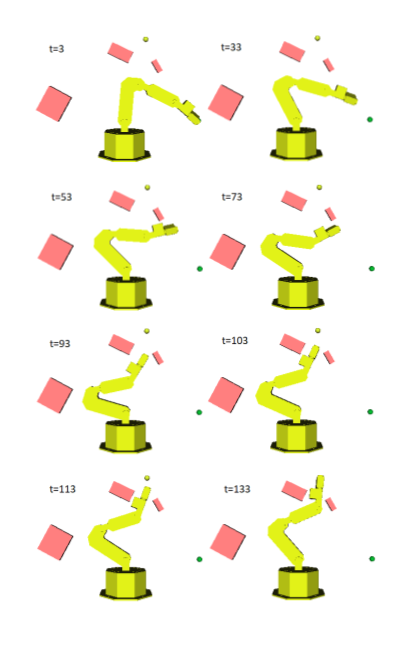
resulting in novel goal-based algorithms. Finally, we apply our method to neural motion
planning, where we demonstrate significant improvements compared to standard RL on
navigating a 7-DoF robot arm between obstacles.